The State of Quantum Computing Systems
The Electronic Numerical Integrator Analyzer and Computer, or the ENIAC as information technology is commonly known, is a lasting production of the 2nd World War. Information technology is by and large credited with starting the modern computing age, fifty-fifty though its original purpose was much more computationally modest, intended as a ballistics estimator for WWII.
The 30-ton computer consumed 160 kilowatts of electric power, took upwardly more than 1,800 sq anxiety (167 sq meters), and independent more than 17,000 vacuum tubes. Information technology could perform v,000 additions, 357 multiplications, or 38 divisions per second, an unprecedented feat at the fourth dimension. However, its true advantage and novelty was that information technology was the first programmable automobile, and could be used besides its original purpose.
It took roughly 50 years between the invention of the vacuum tube transistor and the ENIAC to be built; even so, the realization of the programmable system opened the doors for the man to attain the moon...
A programmable environment opens upwards the door for innovators beyond unlike fields to take advantage of the underlying computing fabric. It took roughly 50 years between the invention of the vacuum tube transistor and the ENIAC to be built; however, the realization of the programmable system opened the doors for the homo to achieve the moon, a myriad of medical techniques and technologies, and an unprecedented turnaround time for vaccine development.

Quantum computing "systems" are notwithstanding in development, and as such the entire arrangement image is in flux. While the race to quantum supremacy amid nations and companies is picking upward footstep, information technology'southward still at a very early stage to call it a "competition."
There are just a few potential qubit technologies accounted applied, the programming surroundings is nascent with abstractions that accept still not been fully developed, and there are relatively few (admitting extremely exciting) quantum algorithms known to scientists and practitioners. Part of the claiming is that it is very difficult and nearly impractical to simulate quantum applications and engineering on classical computers -- doing so would imply that classical computers have themselves outperformed their breakthrough counterparts!

Nevertheless, governments are pouring funding into this field to help push humanity to the side by side big era in computing. The past decade has shown an impressive proceeds in qubit technologies, breakthrough circuits and compilation techniques are being realized, and the progress is leading to even more (good) competition towards the realization of full fledged quantum computers.
ICYMI: What is Quantum Calculating?
In our first article of this two-part series, nosotros focused on the concrete aspects which make breakthrough computing attracting fundamentally to researchers today, and the potential technical and societal benefits making information technology a worthy investment.
In this article, nosotros'll focus on the quantum computing stack, exploring the recent developments in qubit technologies, how they can be programmed for computations, and the challenges and open questions in the field.
Permit's dive correct in!
Recap of Fundamentals
In the first office of this serial, we discussed diverse aspects which make classical computing fundamentally different from quantum calculating. We encourage yous to go over that article for more details, but a few bones takeaways are:
- Quantum bits (qubits) are not binary: they are a superposition of both 0 and 1 values, and thus are much more than expressive than a classical digital fleck.
- Qubits exhibit a property known as entanglement. This property means that two (or more than) qubits are intrinsically associated with i some other. Einstein defined this as "spooky action at a altitude."
- Qubits decohere over time. In other words, maintaining the value of qubits is a fundamental challenge for the realization of fault tolerant (FT) breakthrough systems of the future.
Given these physical building blocks, what types of technologies can actually take reward of these properties?

Qubit Technologies
Designing qubits for a quantum estimator is no simple task. Quantum systems crave very strict isolation of particles and an ability to dispense circuitous physical systems to a level of precision never attempted before.
There are a few competing technologies that have come up up in recent years, including trapped ion qubits, superconducting qubits, semiconductor spin qubits, linear optics, and Majorana qubits. The general philosophy of qubit design tin can be summarized by the following few points (called the DiVincenzo criteria):
- Well-characterized qubits for a scalable system
- Power to initialize qubits (for ciphering)
- Stability of qubits (i.e., long decoherence times)
- Back up for universal educational activity set for arbitrary computation
- Power to mensurate qubits (i.eastward., readout in computational basis)
Interestingly, these goals are in tension with one some other -- as if quantum computing wasn't complex enough! Specifically, initializing and performing computations on a qubit crave interactions on the system, which will inherently intermission the required isolation of making a qubit stable. This is one reason why it is fundamentally difficult to build a quantum computer.
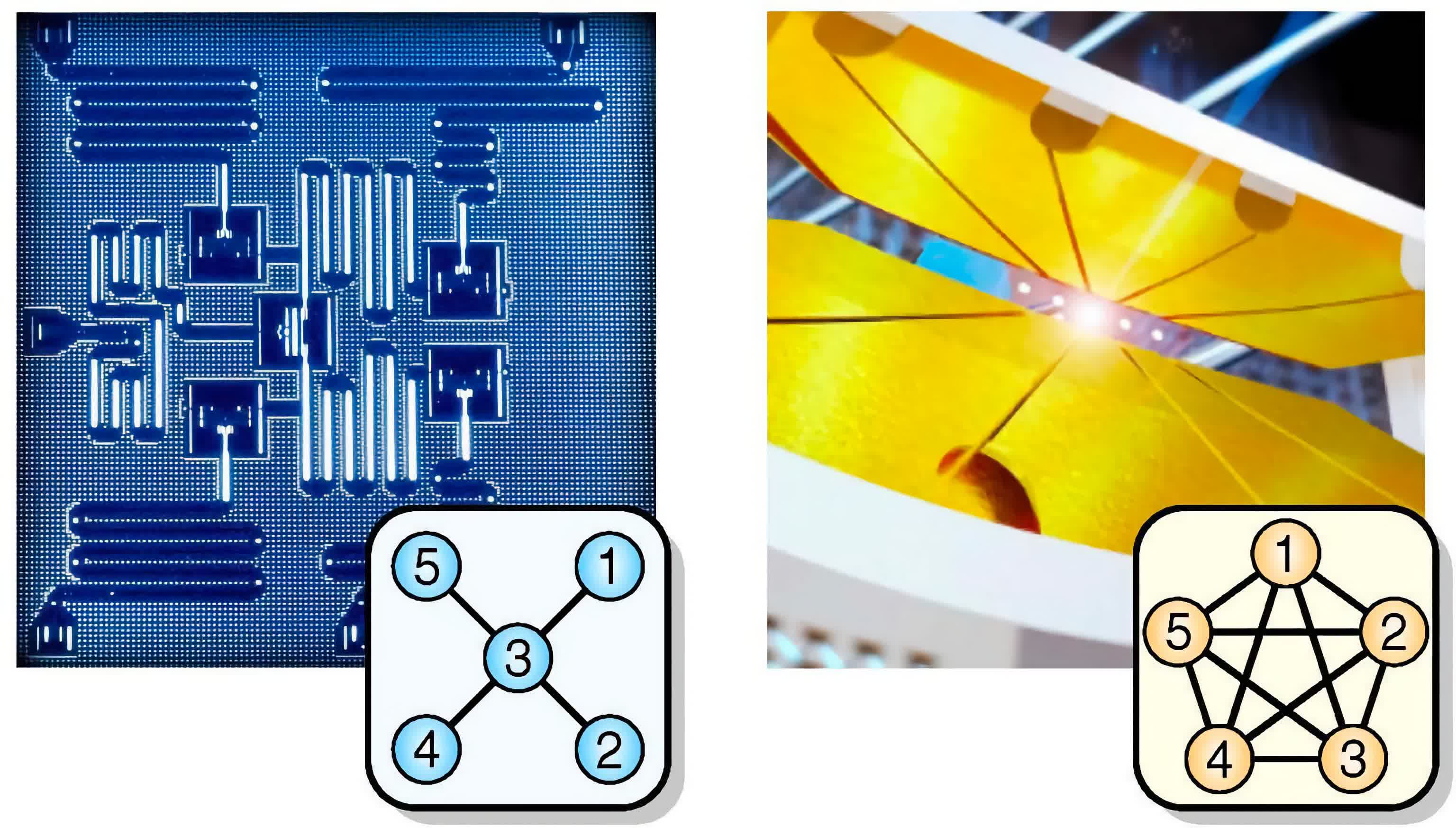
Nevertheless, the two almost promising candidates for NISQ-era (noisy intermediate-scale quantum) bits have been the trapped-ion qubit and the superconducting qubit.
Trapped-Ion Qubits
A trapped ion qubit operates on atoms. Since such a qubit uses the properties of atomic ions, it tin naturally leverage the quantum mechanical properties via internal free energy levels of the atoms. Common ions such every bit Ca+, Ba+, Yb+ (amongst many others) can be used.
Conceptually, the idea is to specify two atomic free energy levels of the ion, and denote those as the 0 and 1 energy levels. The choice of the two levels determines how the qubit is controlled: a large separation betwixt the energy levels (e.g., ten^15 Hz, effectually the frequency of light) means the use of laser beams to excite ions and move them from one land to some other. These are chosen optical qubits.

Hyperfine qubits, on the other hand, have a smaller energy separation (around 10^x Hz). This latter type falls in the microwave frequency, and thus can exist controlled via microwave pulses. The advantage of microwave controlled single-qubit gates is its lower error rate (10^-half-dozen), while the disadvantage is that it is hard to focus on individual ions due to the large wavelength.
How can you stabilize an ion and use it for computation? As the name implies, yous demand to "trap it" to go along it in place to control it. This tin be washed by applying an electromagnetic field in a detail way (an RF Paul trap) to freeze the ion at a saddle point. Once "trapped", the ions demand to be physically cooled to reduce vibrations and decoherence. Every bit you lot might imagine, such a setup would need many components, including lasers, control electronics, liquid helium for cooling, and an farthermost level of precision during performance.
Trapped-Ion qubits are gaining quite the fanfare recently. On Oct i, 2022, IonQ (a Academy of Maryland spin-out firm) was publicly listed on the NYSE. While the theoretical foundations take been around since 1995, but recently has its implementation really taken off.
Additionally, their lower mistake rates provide a compelling technology to be the qubit of the future during the NISQ era. While this is all promising, trapped-ion qubits practise have some drawbacks, the biggest of which is that they are slower than superconducting qubits. This characteristic may be of import to account for real-time errors coming out of the system. Additionally, at that place are limits to how many ions can fit in a single trap and be made to interact. All this does not detract from the promise of trapped-ion qubits.
Superconducting Qubits
In contrast to trapped-ion qubits, a superconducting qubit is implemented with lithographically printed circuit elements. Essentially, these are "artificial atoms" with desired quantum mechanical properties. Until the recent rise of trapped-ion qubit technology, superconducting qubits have attracted significant industrial attention since it more than closely follows existing integrated circuit engineering science.
A superconducting qubit revolves around an electric circuit element chosen a Josephson junction, which is essentially an insulator in between two superconductors. Beneath a critical temperature, the superconductor resistance is dropped to zero, forming a pair of electrons known equally Cooper pairs.

Traditional electrons have +-½ spin (known as fermions), while Cooper pairs take a total spin of 0 (bosons). In a Josephson junction, cooper pairs can quantum tunnel, and give ascent to discrete energy levels needed to make a qubit. The number of Cooper pairs tunneling across the junction relates to the quantum state. There are multiple types of superconducting qubits, including charge qubits, flux qubit, and stage qubit, which differ in their circuit designs and (in turn) their operation and physical mechanisms to implement, command, and measure a qubit.
Superconducting qubits have opened the door for diverse technologies, including silicon-based spin qubits, and have had industrial bankroll for longer than trapped-ion qubits. There is no articulate victor in the engineering infinite at this point: each tech has its own advantages with various backers. At the same time, fundamental limitations will help push more innovation on all fronts to place ideal qubits for future quantum computing systems.
Quantum Gates
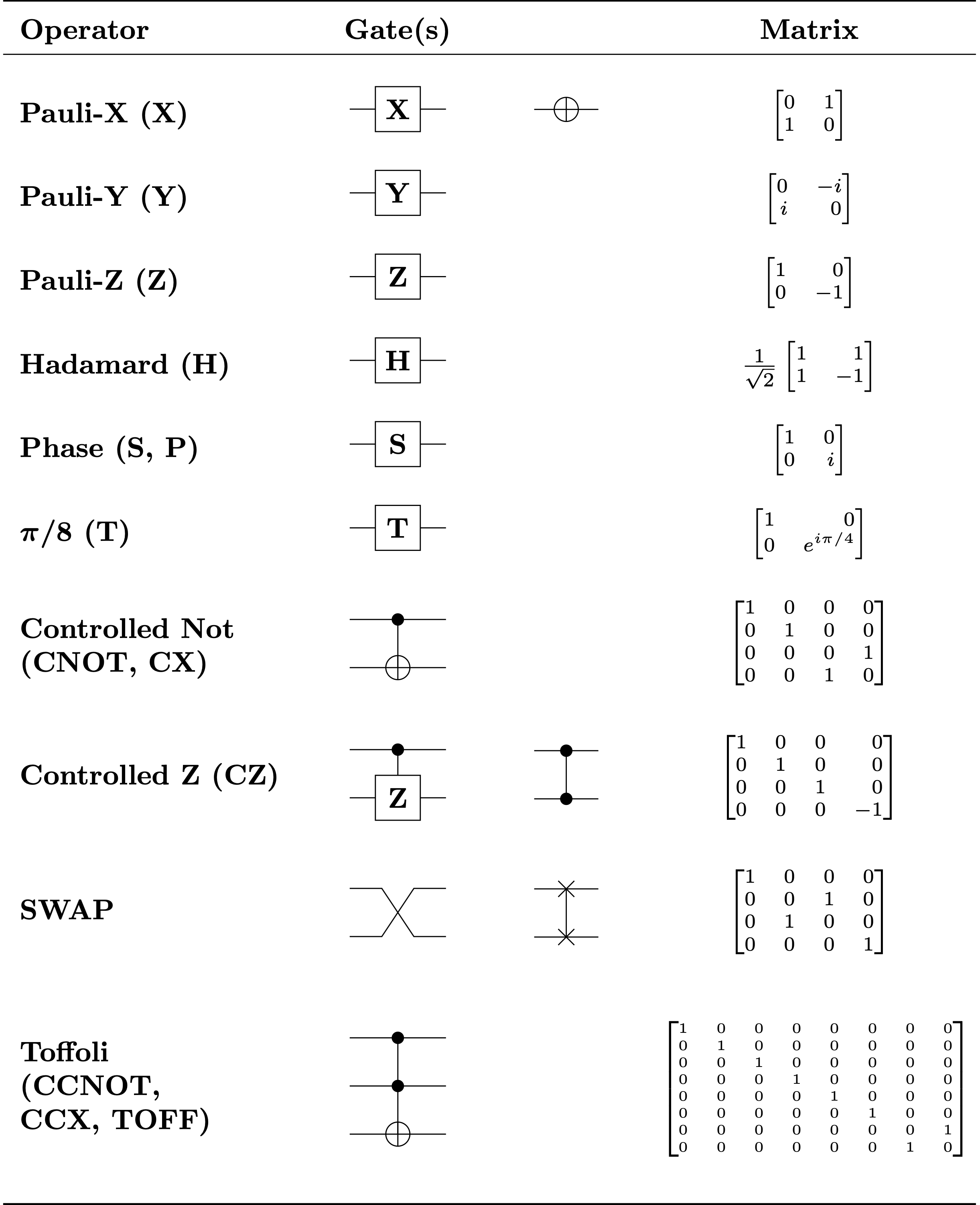
Depending on the qubit applied science, breakthrough logic gates (or more precisely, qubit operations or breakthrough instructions) require different physical operations to process information. A quantum gate is fundamentally a logical transformation represented by unitary matrices.
Retrieve that while classical computations operate under the laws of Boolean algebra, quantum computations operate under the rules of linear algebra. Thus, a transformation/gate is essentially an performance irresolute a qubit's state into another country, which can exist interpreted based on the superposition of its 0 and 1 value.

One unique aspect of breakthrough gates (which sometimes arrive difficult to understand) is that it differs from the classical concept of a Von Neumann architecture. John Von Neumann was a computer architect working on the Manhattan project in the 1940s, when he heard about the ENIAC evolution. He figured out a way to brand the ENIAC much faster, by introducing the concept of a stored-program design. In modern nomenclature, this practically ways separating the memory (for instance, where a program is stored) from the compute units (where information is processed). Such a separation of concerns was instrumental in making machines more productive from a human standpoint -- debugging time can shift to writing better programs, and computer architects tin can focus (almost independently) on improving each of the memory and compute structures for better operation.
A quantum architecture, still, does not have such a unproblematic separation, since the "compute" occurs by concrete transformations on the qubit "retentiveness," and is fundamentally tied to the engineering. While that might seem a flake foreign to a traditional reckoner programmer, it does come up with a unique perk: quantum computers can heavily leverage reversible computations.
A reversible operation is ane where the transition function maps old computational states to new ones is a ane-to-ane function. In other words, knowing the output logic states uniquely determines the input logic states of the computational operation. For example, a Non gate is a reversible function, operating on i bit (or qubit). By extension, a controlled-Non gate (or CNOT) gate uses two logical bits/qubits, where the 2nd fleck controls how/when the NOT gate is flipped. As an analogy, a CNOT gate can be thought of as a reversible XOR gate. Adding one more control bit/qubit introduces the Toffoli gate, where yous can command the control flake going into a CNOT gate.
How is this useful and relevant to quantum computing? Well, the Toffoli gate is a universal reversible computation, meaning that you can implement any (maybe non-reversible) Boolean logic circuit solely using Toffoli gates. In the Von Neumann computing design, this is like to a NAND gate (Not-AND), and its generalizability is a reason why we can plan a computer today to perform practically any ciphering (and perform millions of them very chop-chop).
Simply why end at reversible computations? Another important element of quantum gates is their association with randomized computations. Many classical algorithms have advantage of randomization, since the natural world behaves unpredictably and (to a certain extent) statistically. Quantum computing has that broiled in already, as randomness is a cardinal property closely linked to superposition.
In other words, when measuring a quantum system, you crave many computations (all of which take inherent randomness due to atomic properties), and your output is a probability distribution of the samples you lot made to capture the result. While it seems similar a new model of computing, it is really closer to the fundamental nature of the world as very few things in the globe are certain (with the exception of decease and taxes as Benjamin Franklin said in 1789).
Other popular quantum gates (not discussed here but highly relevant) are the Hadamard gate, the Controlled Hadamard gate, a Pauli gate, a SWAP gate, a controlled SWAP gate, and others (exercise you meet a pattern?). While these are important for diverse algorithms, the master takeaway is that these gates are essentially linear algebra operations, and tin exist used to transform the country of a qubit for desired computations.
Quantum Compiling
And so far, we've been going "up the stack" in describing a breakthrough computing system: breakthrough physical properties can be captured with qubits, which in plough tin be operated on with various logic gates for information processing, with the high-level objective of implementing a quantum algorithm. The connectedness between the high-level quantum algorithm and the low-level breakthrough hardware requires the realization of a quantum compiler. A quantum compiler is a series of transformations and optimizations on a breakthrough intermediate representation (QIR) of a program.
Let's unpack that jargon a bit.
In the classical sense, a compiler is a slice of software that is tasked with transforming a loftier-level programming language (such as C++, Python, etc.) into a machine-defined education set architecture or ISA (such as x86, ARM, Power, RISC-V, etc.) The ISA forms the contract between the programmer and the machine, allowing users to write code which a compiler then "translates" for the machine to understand. The motorcar then executes the instructions to execute the program on the automobile, using the compiled "recipe."

The pedagogy set of a quantum reckoner are the gates described in a higher place: CNOT gates, Hadamard gates, "Clifford+T" gates, and other operations on qubits. However, a quantum compiler'south job is more circuitous than merely "translating" a college level language (examples include cQASM, Quil, and Q#) into a serial of gates. It likewise has to take into consideration the breakthrough physics of the underlying computations.
For example, qubits tin can be entangled, then their interactions need to exist scheduled appropriately. Qubits also decohere over time; thus you need an optimal configuration to reduce (and take into consideration) the noisy nature of the operations. Interactions betwixt qubits might also be limited by the underlying technology: non all qubits can interact with ane another physically, and thus the compiler needs to be enlightened of hardware constraints when implementing an algorithm. In case this didn't seem similar plenty piece of work for a quantum compiler, a highly remarkable phenomenon known as quantum teleportation increases the complication farther. Quantum teleportation leverages entanglement to transfer information beyond "far abroad" qubits. While seemingly far-fetched, this characteristic can assistance reduce communication costs via scheduling, but of course, it needs to be properly managed by the organization.
If this all seems likewise much to encompass at once - you lot're not solitary! Quantum compiling is a hot research area precisely for all the complexities involved. While classical computer systems have been designed with squeamish abstractions enabling innovations at split up levels in the computing stack, the breakthrough calculating "system" is very much still in flux.
To quote Dr. Yongshan Ding and Dr. Fred Chong from the University of Chicago, "the primal to successful execution of quantum algorithms on NISQ devices is to selectively share information across layers of the stack, such that programs can use the limited qubits most efficiently." Quantum compilation aims to do that for united states of america; yet, information technology is still very much at a nascent phase itself.
Fault Tolerance and Dissonance Mitigation
Today, quantum computing is very much synonymous with fault tolerance and racket mitigation -- information technology is quite literally in the proper name: noisy intermediate-scale quantum (NISQ) computers.
Most qubits in a organization are being used to annul the decoherence of the quantum arrangement, and recoup physically and algorithmically for computing faults.
The primary metric used to measure out how long a quantum state tin can last is aptly called the coherence time. For reference, modern day coherence time is measured in the order of minutes to roughly one hour. Imagine if each bit in your current processor randomly flips its value every hr... getting anything (useful) done would be quite impractical!
That said, given the processing power of a quantum scrap, y'all tin really perform many computations (i.e., qubit transformations) within such a fourth dimension frame, but it is much less feasible to execute long-running algorithms exhibiting breakthrough supremacy.
Ane of the common techniques today to mitigate the natural decoherence of qubits during ciphering is to use redundancy, much similar classical systems. Specifically, quantum error code correction (QECC) substantially mirrors modern ECC, where additional (qu)bits are expended to discover if an error occurred and to correct it. A common quantum error correcting code is the ix-bit Shor code (or simply, the Shor Code), where ane logical qubit is encoded using 9 physical qubits that can right for arbitrary errors in a single qubit. In other words, for every qubit in your system doing "useful" computations, you'd need an extra 8 to brand sure information technology is operating properly.
QECC isn't the but mode to address faults in a quantum system. Another method is randomized compiling. The idea is to insert random gates into a quantum circuit, and boilerplate over many of those independently sampled random circuits. While the effect of racket on the individual circuit may be unlike, the expected racket on multiple random circuits is tailored into a stochastic form. Essentially, you can utilise clever math to recoup while incorporating error directly in the computations.
The quantum compiler can as well perform various mapping smarts to account for errors, such as minimizing cross-talk between qubits during hardware circuit translation, recalibration of the organisation error charge per unit and remapping qubits, and minimizing the circuit length to "speed up" the computations before decoherence takes over.
All these techniques exist because of the imprecise command of breakthrough hardware and natural decoherence of states. While many of these techniques are specific to the NISQ era, a major goal is to ameliorate empathise errors and mitigate them for the eventual Mistake Tolerant (FT) era of quantum computers.
Many believe that the FT era is when quantum supremacy tin can actually be realized for many applications.
Summary and Takeaways
We've come a long way in the development of quantum computers, with many companies and research facilities pushing the envelope in fully capturing the quantum backdrop of our universe. While many of the foundational theories are now being implemented, total quantum "systems" remain in agile development.
Competing qubit technologies, noisy systems and decoherence, and an incredible "do-all" compiler are still challenges for the race to breakthrough supremacy. Furthermore, the NISQ era we are currently experiencing and the hereafter FT era might expect vastly unlike. The modernistic computing "stack" is even so in early evolution, and many new and exciting quantum technologies are sure to arrive in the most future.
While breakthrough computing has not taken the globe by a tempest (all the same), one tin imagine the benefits and consequences of having breakthrough computers at our disposal. While the foundations of quantum mechanics are almost a century old, researchers and practitioners are at present beginning to actually design these systems and solve many fascinating research and applied science challenges. With many players at present invested in the quantum race, the number of qubits in a organisation is increasing practically every other day, and information technology will only be a matter of fourth dimension before truly fault-tolerant systems are a reality.
Source: https://www.techspot.com/news/92215-state-quantum-computing-systems-current-designs-future-challenges.html
Posted by: andersonwhishis.blogspot.com


0 Response to "The State of Quantum Computing Systems"
Post a Comment